Matériaux de basse dimensionalité

Matériaux de basse dimensionalité

La théorie de la fonctionnelle de la densité (TDDFT) est une formalisme ab initio extrêmement puissant pour simuler les excitations électroniques des matériaux. Bien qu’il s’agisse d’un formalisme longitudinal, il permet la description du spectre d’absorption, qui est la réponse à un champ transverse. La théorie est bien établie pour les cristaux infinis (3D), où les conditions aux limites périodiques suggèrent naturellement de travailler en espace réciproque, et repose sur deux résultats : i) La contraction longitudinale-longitudinale (LL) et transverse-transverse (TT) du tenseur diélectrique macroscopique sont égales dans la limite optique et ii) la contraction LL est égale à l’inverse de la moyenne macroscopique de la fonction diélectrique inverse, qui est la quantité calculée en TDDFT.
Un premier usage du formalisme périodique pour étudier des objets non-périodiques a concerné les surfaces. Plus récemment, la promesse de nouvelles propriétés électroniques émergeant du confinement électronique dans les matériaux de taille nanométrique, a conduit à appliquer ce formalisme aux nano-objets isolés. Pour ces systèmes, pour lesquels la périodicité est partiellement ou totalement supprimée, on construit une supercellule, qui contient la matière et du vide pour isoler l’objet des répliques artificielles résultant de la répétion périodique de la supercellule.
 

Formalisme Selected-G

Dans le cadre de la TDDFT, nous avons mis en évidence que le spectre d’absorption calculé pour une excitation perpendiculaire à la surface n’était pas correct lorsqu’on prenait en compte les effets de champs locaux. Nous avons montré que le pic d’absorption apparaissait au-dessus de 12 eV au lieu de 4 eV pour le matériau massif, et que cette position en énergie ainsi que l’amplitude étaient dépendants du vide introduit dans la supercellule. Nous avons dérivé une expression modifiée de l’équation de Dyson de la TDDFT faisant intervenir des quantités ayant la périodicité de la matière au lieu de celle de la supercellule, et une nouvelle expression du potentiel coulombien. Ce nouveau schéma a été appelé Selected-G. Dans la limite de l’épaisseur de matière infinie, il nous a permis de retrouver le spectre d’absorption correct pour la perturbation perpendiculaire à la surface. Ce formalisme a été appliqué avec succès à la génération de seconde harmonique par des surfaces de silicium.

Ref: Nicolas Tancogne-Dejean , Christine Giorgetti, Valérie Véniard
Optical properties of surfaces with supercell ab initio calculations: Local-field effects
Phys. Rev. B 92, (2015). 
 

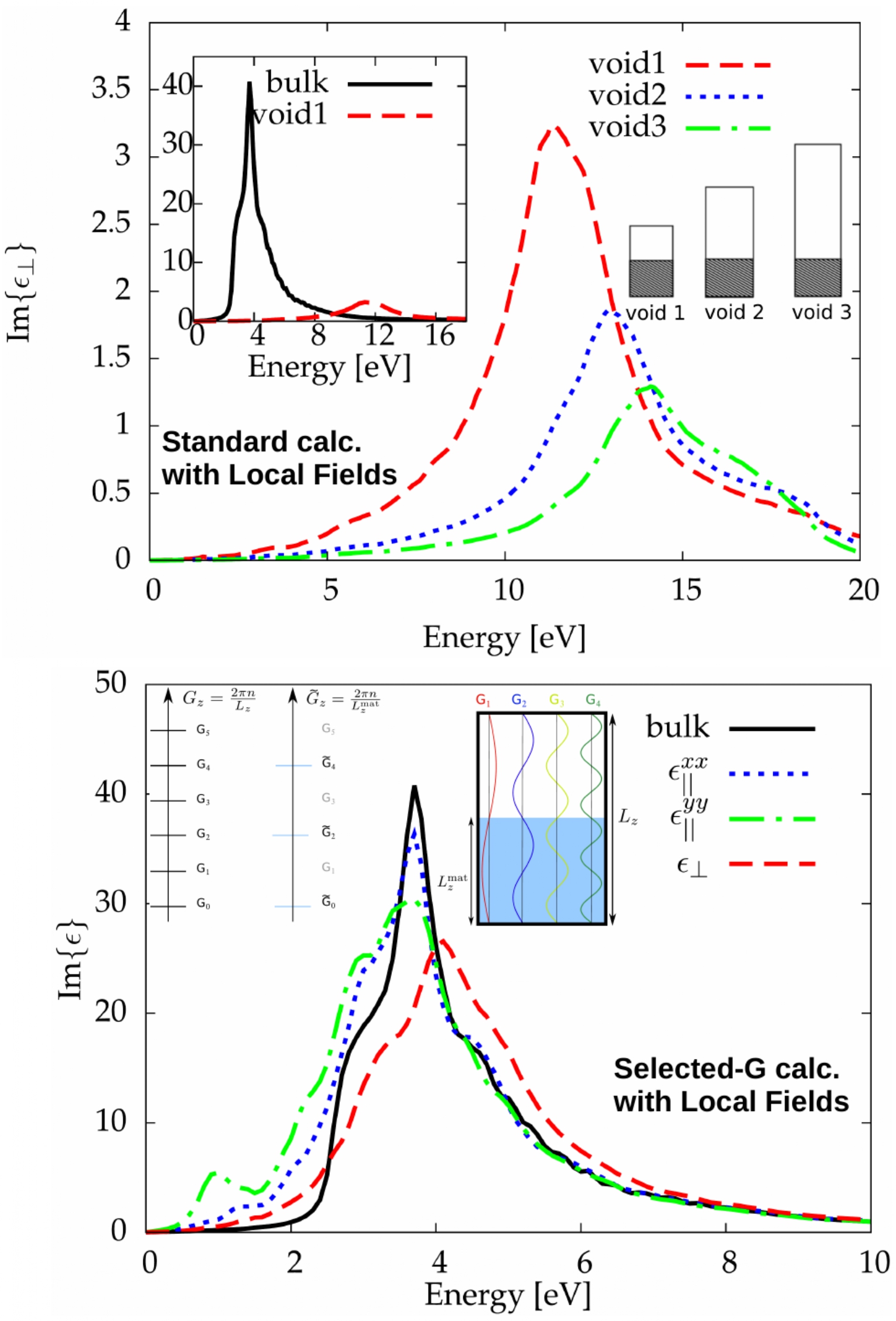
Propriétés optiques d’objets quasi-bidimensionels calculées par la théorie de la fonctionnelle de la densité

Durant la thèse de Stefano Mazzei, en associant l’électromagnétisme classique et la TDDFT en espace mixte et réciproque, nous avons mis en évidence que le formalisme développé pour les objets tridimensionnels ne s’appliquait plus pour les matériaux ultra minces.

Une nouvelle expression de la fonction diélectrique macroscopique

A partir de l’éclairage apporté par le modèle classique de Lorentz, et en utilisant la TDDFT en espace mixte, nous avons démontré la raison pour laquelle, pour une perturbation parallèle au plan de la couche, la moyenne macroscopique de la fonction diélectrique inverse était une quantité pratiquement égale à un, et ne pouvait pas représenter le spectre d’absorption. C’est une conséquence de la forte réduction du champ électrique induit. En repartant de la définition du tenseur macroscopique, et en exploitant cette dernière propriété, nous avons établi la formule qui permet de calculer correctement le spectre d’absorption. 
 

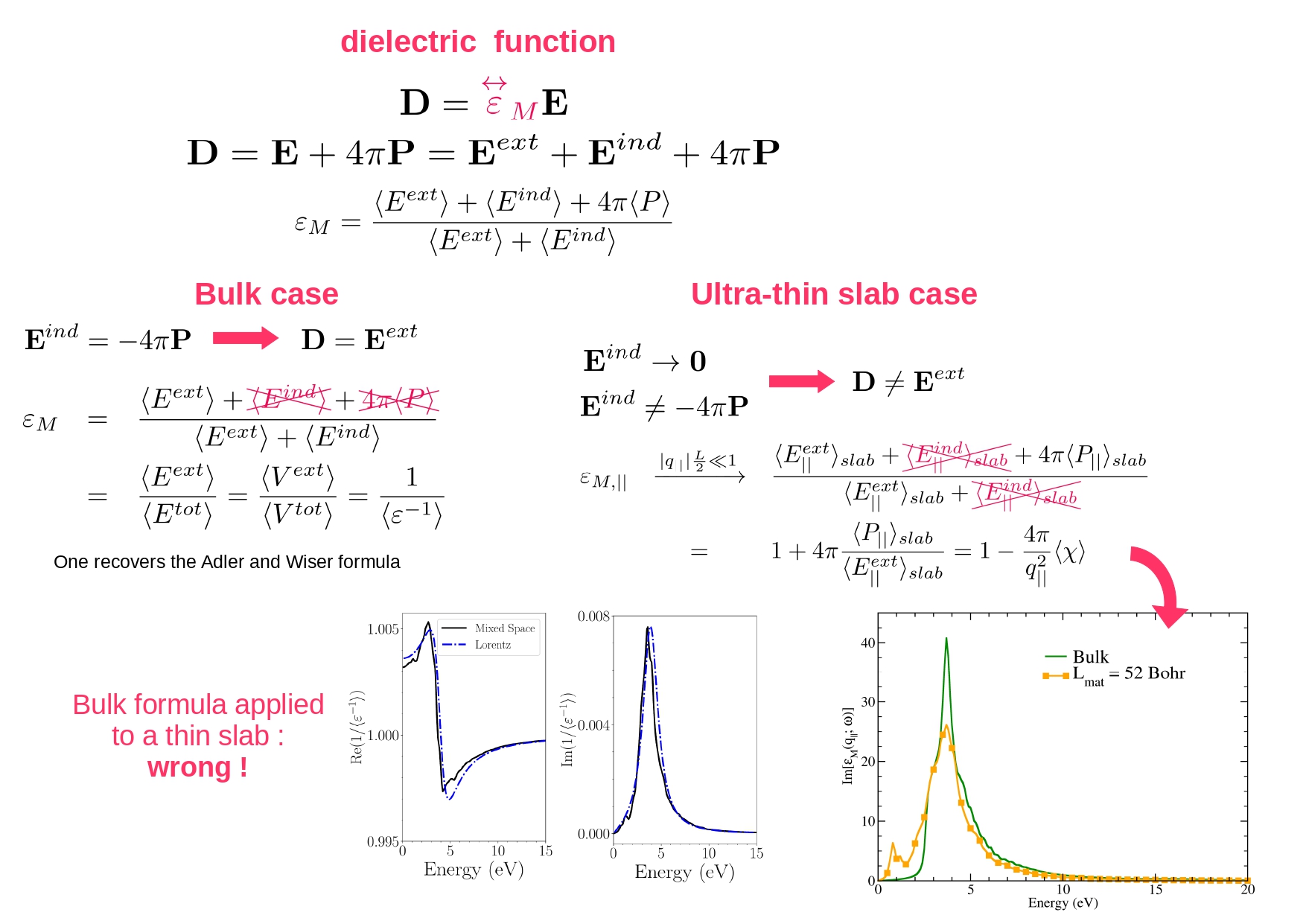
Ref : Stefano Mazzei, Christine Giorgetti 
Optical response of two-dimensional systems: Insights from classical electromagnetism to ab initio calculations 
Phys. Rev. B 106, 035431 (2022).

Fonctions diélectriques transverse et longitudinale

En calculant la fonction de réponse au potentiel macroscopique total, pour une perturbation faisant un angle arbitraire avec le plan de l’objet quasi-2D, nous avons établi que le fait d’inclure les interfaces avec le vide dans la définition de l’épaisseur de l’objet change complètement la nature des propriétés. Nous avons montré que la fonction de réponse de la couche ultra-mince est une combinaison linéaire de deux contributions : une résonance à la fréquence d’absorption associée à la projection de la perturbation dans le plan, et un pic à la fréquence plasmon du matériau massif correspondant, pour la projection de la perturbation perpendiculaire au plan. Ce résultat inattendu a été clarifié grâce au modèle classique d’Airy dans la limite d’une couche ultra-mince. En effet, nous avons mis en évidence que la transmittance, la réflectance et l’absorbance d’un tel objet présentent les mêmes caractéristiques. Ceci nous a permis de conclure que i) pour une perturbation perpendiculaire au plan, la contraction longitudinale du tenseur diélectrique, qui se trouve être le plasmon, n’est plus égale à la contraction transverse, qui donne le spectre d’absorption. ii) le formalisme longitudinal de la TDDFT peut toujours être utilisé pour calculer la réponse optique, par nature transverse, mais qui n’est pas la contraction transverse du tenseur diélectrique. 
 

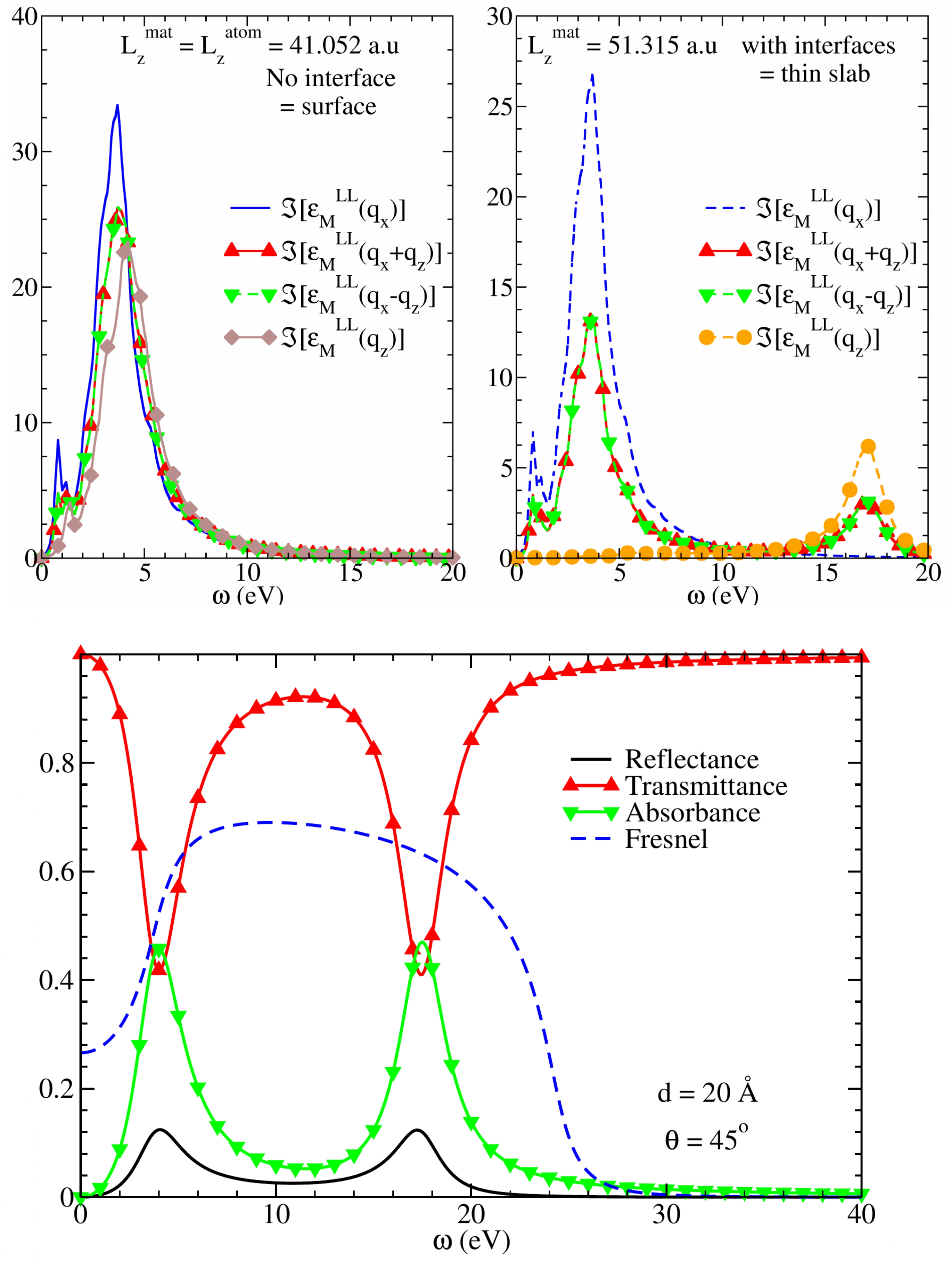
Ref :Stefano Mazzei, Christine Giorgetti
Optical properties of quasi-two-dimensional objects from time dependent - density functional theory: longitudinal versus transverse dielectric functions
Phys. Rev. B 107, 165412 (2023).

contact christine.giorgetti@polytechnique.edu